
Part 2 of the Dualism, Monism & Thelema Series
For there to exist a dualism between two terms, there must be a distinction to be made between them. Likewise, to speak of the same two things from a monistic perspective means in some sense to deny the distinction between them.
The philosophical tradition has acknowledged at least three kinds of distinctions since the time of Descartes in the 17th century: real distinctions, modal distinctions, and rational distinctions.
In order to understand the three kinds of distinctions, it’s necessary to understand the terminology Descartes used to talk about substances and properties.
Substances and their Properties
Substances
A substance is anything that does not depend on anything else for its existence.
Strictly speaking, from Descartes’s perspective, God is the only substance, since all things come from God and depend upon His continual support. More loosely speaking, though, anything that depends only on God for its existence could be thought of as a substance.
Under this looser criteria, Descartes recognizes the existence of three substances: God, body, and mind.
Principle Attributes of Substances
Substances can have many properties, but any property which makes the substance the kind of substance it is is called a principle attribute.
We have no idea what the principle attribute of God is, but the principle attribute of body is extension, and the principle attribute of mind is thought.
Principle attribute is just another way of saying essence.
Modes of Substances
A mode is a way of being of a principle attribute of a substance.
For example, shape is a principle attribute of a bodily substance, but being square is a mode.
Thought is a principle attribute of a mental substance, but being preoccupied is a mode.
Having established substances, principle attributes, and modes, let’s see what sorts of distinctions hold between them.
Distinctions between Substances, Principle Attributes, and Modes
Descartes tended to talk about distinctions in terms of the conditions of the existence of substances. I’m going to follow Leibniz instead and talk about the intelligibility of substances.
The Leibnizian school preferred talking about substances in terms of their respective intelligibilities rather than their existences, because otherwise it led to the conclusions of Spinozism, according to which there are no finite, dependent substances.
As it turns out, Crowley is much more of a Leibnizian than a Cartesian or Spinozist. As we’ll see, in order to conceive of multiple Stars, each being “God of Very God,” we will need the concept of a finite, dependent substance.
Real Distinctions

Two things are really distinct if and only if each is intelligible independently of the other. They must be either distinct substances or modes of distinct substances.
For example, I can conceive of (i.e., understand) the properties of a triangle without understanding anything about joy. I don’t ever have to have experienced joy or even heard of it in order to be able to deduce that the interior angles of a triangle add up to 180°. On the other hand, I don’t have to know the first thing about the geometry of triangles in order to know joy.
This is because triangularity and emotion are modes of independent substances (bodily substances and mental substances, respectively).
If we’re not being too strict, we could also say I don’t need to understand how to play chess in order to know how to drive (and vice versa). They are really distinct disciplines.
One of the implications of two things being really distinct is that negating one has no impact on the other.
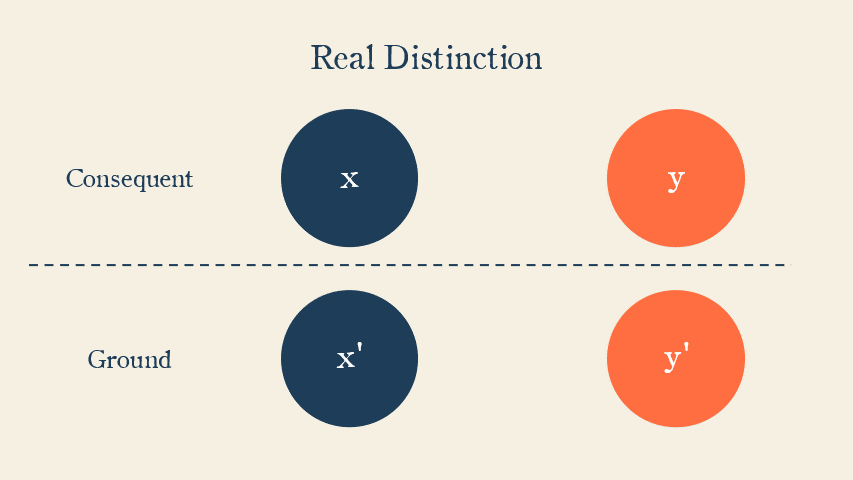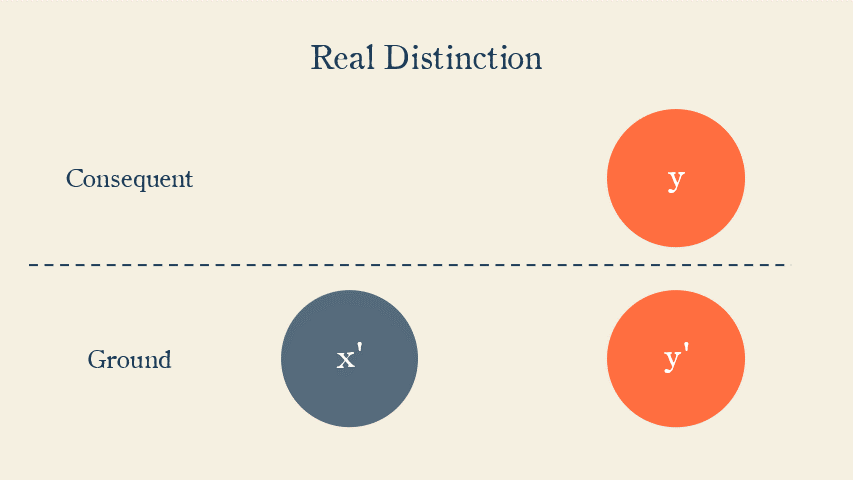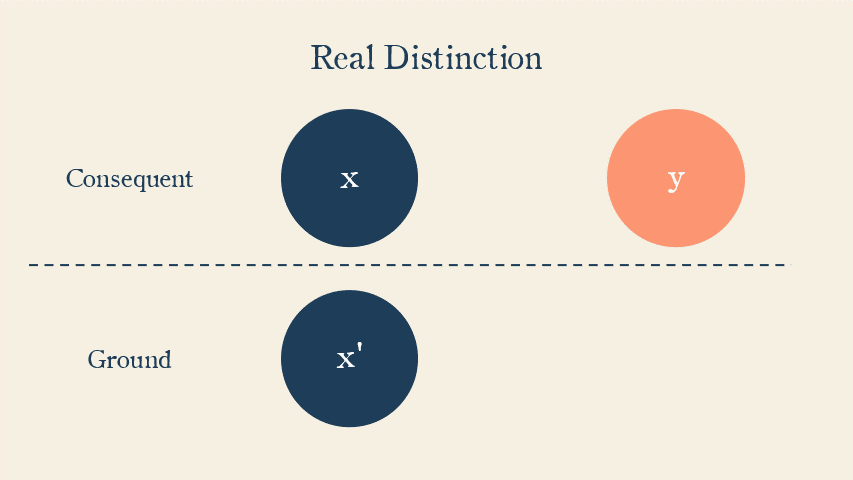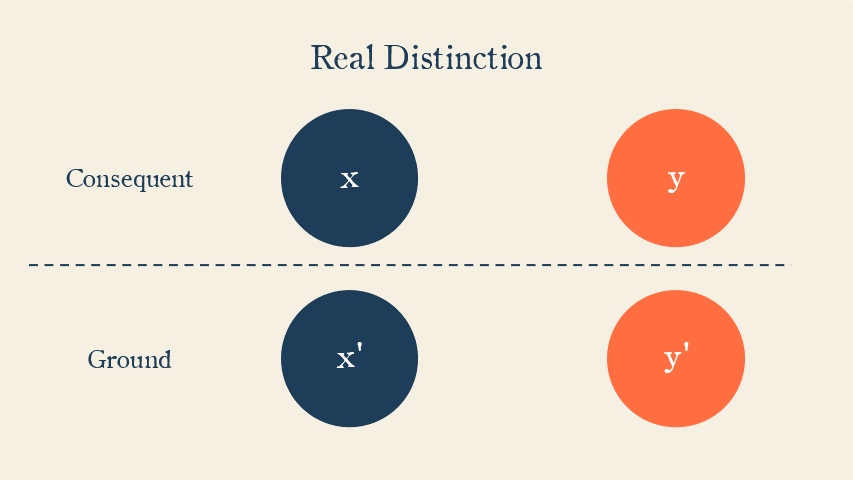
Another implication is that, if x and y are really distinct, and if the ground of x is x’ and the ground of y is y’, then negating x’ has no impact on y, and negating y’ has no impact on x.
For example, the knowledge of trigometry (x) is based in the knowledge of geometry (x’). The knowledge of joy (y) is based in the knowledge of happiness (y’). Having never known happiness has no necessary impact on my understanding of trigometry, and having never known geometry has no necessary impact on my knowledge of joy.
Modal Distinctions

Two things are modally distinct if and only if (a) one is intelligible independently of the other but not vice versa, or, (b) either can exist without the other, but they have a necessary condition of their intelligibility in common.
Modal distinctions hold between (a) the essential property of a substance and a mode of the same substance, or, (b) between modes of the same substance.
An example of a modal distinction of the (a)-type is the distinction between being square (y) and having a shape (x). Shape is the essential property of a bodily substance. Being square is a mode or modification of shape. I can conceive of shape without knowing anything about squares in particular, but the reverse does not hold.
This is called a relationship of ground (x) and consequent (y). The negation of x necessarily entails the negation of y, but not vice versa.

The (b)-type modal distinction is between modes of the same substance.
For example, I was surprised when I got to college and realized I could do calculus without having to do algebra. (The teacher didn’t care if we reduced our answers.)
It’s not that algebra and calculus are really distinct, though. They’re modally distinct. Both are modifications of our understanding of number.
Another example of the (b)-type modal distinction is any distinction made between two very different emotions, e.g., love and hate. If I had never experienced the emotion of hate, it would have no impact on my ability to understand love and vice versa.
On the other hand, if I had no understanding at all what an emotion was, I would not be able to understand either.
If we want to speak more loosely, another example is that I don’t need to understand how to play jazz guitar in order to drum (or vice versa), but I need to understand how to keep time to do either.
One of the implications of the (b)-type modal distinction is that if x and y are modally distinct in this sense, then neither is the ground nor consequent of the other. Rather, they are both consequents of the same ground, z. The negation of x will not necessarily entail the negation of y (or vice versa), but the negation of z entails the negation of both x and y.
Another implication of the (b)-type modal distinction is that two things can appear to be really distinct when they are in fact modally distinct in the (b)-type sense.
Rational Distinctions

Two things are rationally distinct if and only if the distinction is being made between the object and itself, considered under two concepts.
In other words, we’re attempting to make a distinction between the substance and its principle attribute.
An example of a rational distinction would be between any bodily substance and its extension, since without extension, a bodily substance is inconceivable.
Modern philosophers talk about the difference between connotation and denotation. The same object (x) can be denoted (basically, referred to) under two connotations (basically, meanings).
The classical example of this is the distinction between Morning Star and Evening Star. These are two different connotations for the same object, the planet Venus.
The kinds of rational distinctions we’re going to look at will look very much like distinctions between different connotations of the same thing.
One of the implications of two things being rationally distinct is that the affirmation or negation of one will necessarily entail the affirmation or negation of the other. This is because they are both referring to (denote) the same thing.
Now that we have some tools, let’s use them to look at exactly what sorts of distinctions hold between:
- Nuit and Hadit.
- Nuit and Hadit and the Star.
- The Star and its Khu.
- One Star and any other Star.