Part 3 of the Dualism, Monism & Thelema Series
Nuit and Hadit as Foundations
The Book of the Law presents Nuit and Hadit as the two exclusive deities of the Thelemic universe.
I am Heaven, and there is no other God than me, and my lord Hadit.
AL I.21
Furthermore Crowley took Nuit and Hadit to constitute the elements of the universe.
The elements are Nuit—Space—that is, the total of possibilities of every kind—and Hadit, any point which has experience of these possibilities. (This idea is for literary convenience symbolized by the Egyptian Goddess Nuit, a woman bending over like the Arch of the Night Sky. Hadit is symbolized as a Winged Globe at the heart of Nuit.)
“Introduction” to the Book of the Law
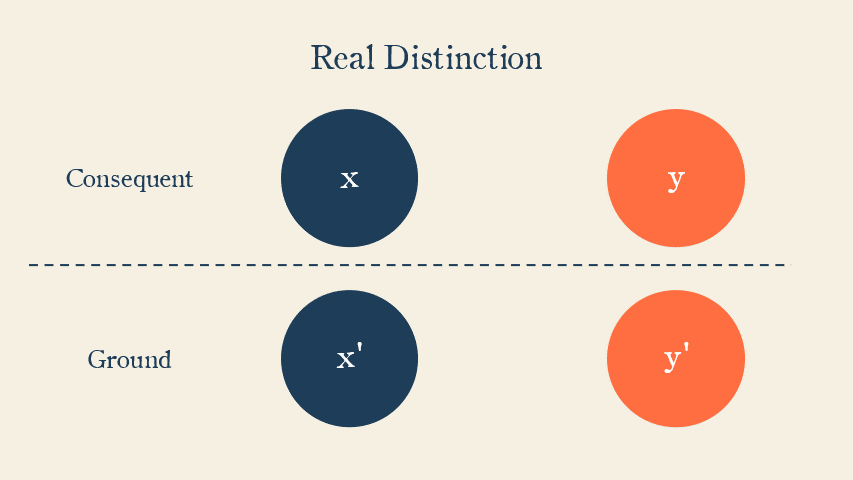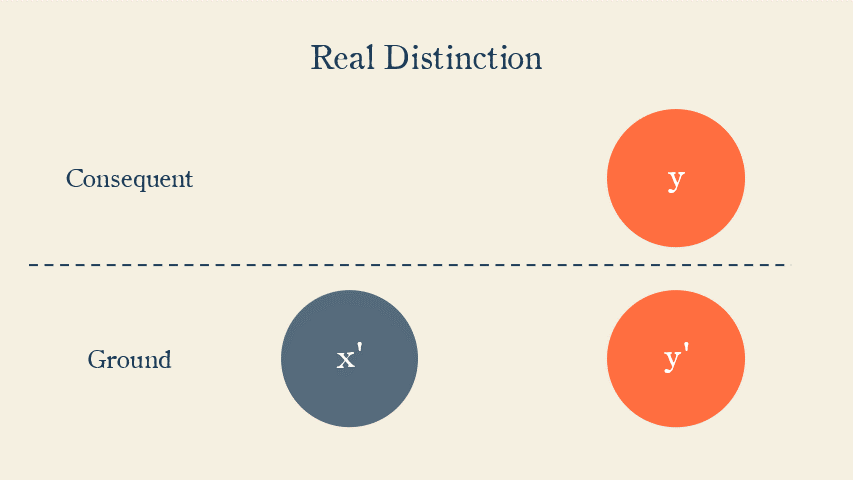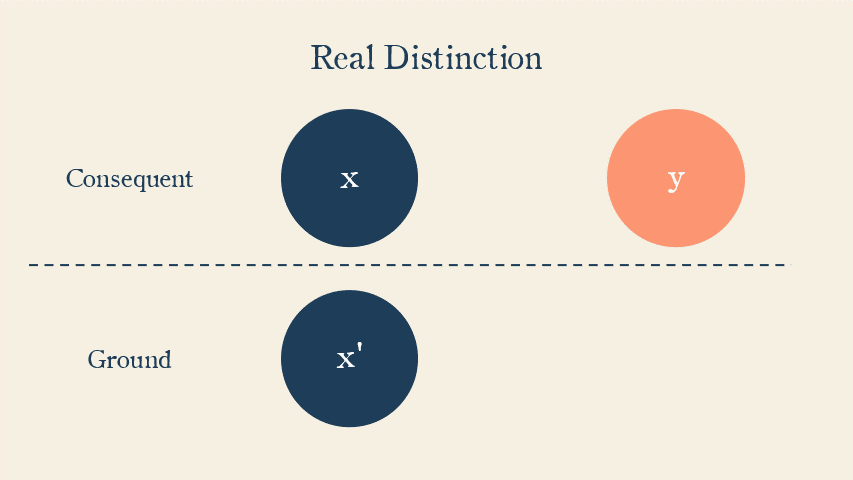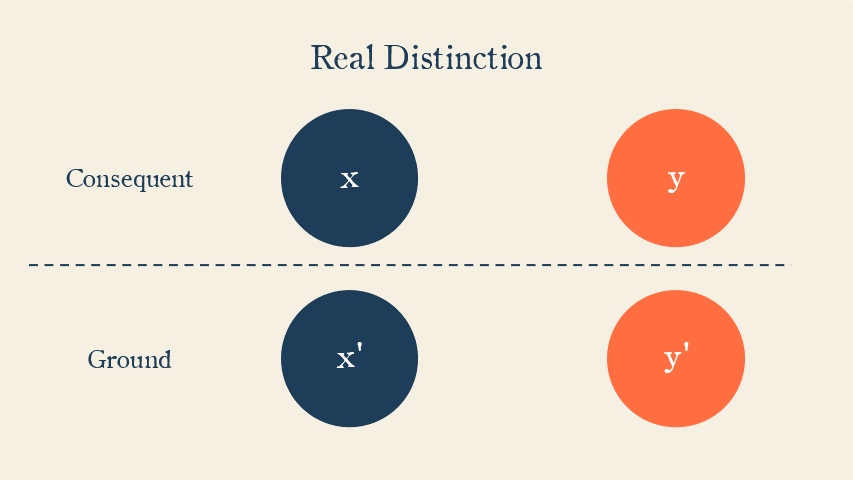
If Nuit and Hadit are both exclusive and elementary, then in our established terminology, they appear to be really distinct substances.
Forming a clear, distinct idea of space as distinct from the subjective point of view presents no difficulty. In fact they seem close in meaning to Descartes’s bodily substance and mental substance respectively.
This would appear to commit Crowley to mind-body dualism and make the Thelemic cosmology dualistic.
The Qabalistic Zero as Common Condition

Nuit and Hadit separating from the Cosmic Egg
However, in Crowley’s early essay, “Berashith,” he lays a framework for deriving Nuit and Hadit from an ontologically prior “nothingness”.
I assert the absoluteness of the Qabalistic Zero […] Our Cosmic Egg, then, from which the present universe arose, was Nothingness, extended in no categories
Crowley, “Berashith”
He then goes on to describe the creation of the universe in terms that anticipate the Thelemic cosmology of Magick in Theory and Practice chapter 0, where the infinitely great (Nuit) and the infinitely small (Hadit) combine to create Ra-Hoor-Khuit. (Magick, p. xxvii and p. 137. All references to Magick will be to the Weiser Second Edition, ed. by Hymenaeus Beta.)
So while there appears to be a real distinction between Nuit and Hadit, they share a common necessary condition in the Qabalistic Zero, which makes them modally distinct.
This implies that, while Thelemic cosmology initially appears dualistic, it is in fact monistic. All things are One (or “None,” as Crowley says) in the Qabalistic Zero.
But we need to make a distinction between two kinds of monism.
Identity Monism versus Dependence Monism

Identity monism entails a rational distinction
If two things are rationally distinct, then the difference is only in the concept we are applying to them. They are in fact one and the same thing. Let’s call this identity monism.
Crowley is not saying that the distinction between Hadit and Nuit is merely a rational distinction. Therefore we are not dealing here with a case of identity monism.

Dependence monism entails a type-b modal distinction
Instead, Crowley is implying that Hadit and Nuit are modally distinct: one is intelligible without the other, but they share a common third condition—the Qabalistic Zero—upon which they are mutually dependent.
So instead of calling this identity monism, I will follow Paul Franks and call this an instance of dependence monism. (Paul Frank, All or Nothing: Systematicity, Transcendental Arguments, and Skepticism in German Idealism, Harvard University Press, 2005.)
The implication is that, while Hadit and Nuit share a common condition in the Qabalistic Zero and hence are not really distinct substances, they are distinct modes of a single substance, and therefore the interaction between them is not illusory.
This is relevant to Crowley’s critique of “mystic monism” and its denial of the “interplay” of parts.
This is something the same as mystic monism, but the objection to that theory is that God has to create things which are all parts of himself, so that their interplay is false.
New Comment on AL I.3
In the context of this quote, Crowley is referring specifically to the interplay of Stars, but the point applies equally to the interplay of Nuit and Hadit.
Further, we can clarify his meaning of “mystic monism” in this passage. He is referring to what we are defining as identity monism, not necessarily all kinds of monism.
This is important, because it is only by committing himself to certain types of monism that other aspects of Thelema remain intelligible. This is especially true of its soteriology, which we saw previously requires the individual to transcend duality.
Is the Qabalistic Zero a Substance?
One might object to my line of reasoning thus far in the following way:
- A modal distinction between x and y assumes x and y are modes of a substance, z.
- A substance is a being.
- The Qabalistic Zero is defined as “Nothingness, extended in no categories,” i.e., the opposite of a being.
- Therefore, Nuit and Hadit cannot be considered modes of the Qabalistic Zero.
But for the purposes of our argument, we are defining substance as intelligible on its own terms. It’s defined without reference to existence.
The Qabalistic Zero is intelligible. This is evidenced in “Berashith” and later in Chapter 5 of Magick Without Tears, where Crowley provides a mathematical proof of the common origin of Nuit and Hadit in the Qabalistic Zero.
Not only that. He infers certain of their characteristics (like that Nuit is infinitely great and Hadit infinitely small). It’s impossible to make inferences from something if it’s unintelligible.
The particulars of the argument—which constitute the 0=2 theorem—need not preoccupy us. All we need understand is that Crowley treated the Qabalistic Zero as the intelligible, common ground of Nuit and Hadit.
Derivation Monism versus Dependence Monism
Since by Crowley’s lights the respective existences and qualities of Nuit and Hadit can be derived using logic and mathematics from their common condition, in addition to describing this as a form of dependence monism, I will again follow Franks and describe this as an example of derivation monism.
Not all examples of dependence monism are also examples of derivation monism. We might know that x is the necessary condition of y, and hence there exists a modal distinction between x and y, but it does not necessarily follow that we can know the particular qualities of y through examining x (or vice versa).
In other words we might identify x as the condition of the intelligibility of y without being able to explain or reduce all of the qualities of y to x.
For example, a triangle is a modification of shape, but it does not follow that we can deduce the sum of the interior angles of a triangle solely by means of an examination of the meaning of shape.
This distinction will be essential to make sense of Crowley’s thoughts about the Star.
To summarize:
- Hadit and Nuit are the dual foundations of Thelemic cosmology.
- Hadit and Nuit share a common condition in the Qabalistic Zero.
- So the distinction between Hadit and Nuit is modal, not rational. They are intelligible independently of one another but mutually depend upon the Qabalistic Zero. This is an example of dependence monism, not identity monism.
- Certain qualities of Nuit and Hadit can be derived from the Qabalistic Zero. This is an example of derivation monism.
- Not all instances of dependence monism are also instances of derivation monism.
Next we’ll look at how Nuit and Hadit are distinct from the Star.